Έστω ένα υλικό σημείο που κινείται με 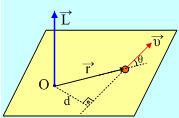 ταχύτητα υ και έστω ένα σημείο Ο.
ταχύτητα υ και έστω ένα σημείο Ο.
Ορίζουμε στροφορμή του υλικού σημείου ως προς το Ο, το εξωτερικό γινόμενο:
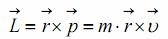 Όπου r η απόσταση του υλικού σημείου από το σημείο Ο.
Όπου r η απόσταση του υλικού σημείου από το σημείο Ο.
Πράγμα που σημαίνει ότι η στροφορμή είναι ένα διάνυσμα, με διεύθυνση κάθετη στο επίπεδο που ορίζουν ο φορέας της ταχύτητας και το σημείο Ο, στο σημείο Ο, φορά που προκύπτει από τον «κανόνα του δεξιόστροφου κοχλία» και μέτρο ίσο μεL=mυr∙|ημθ|, όπου θ η γωνία μεταξύ υ και r (ισοδύναμαL=mυd όπου d η απόσταση του Ο από τον φορέα της ταχύτητας, ορισμός που μας επιτρέπει κατά αναλογία να πούμε, ότι η στροφορμή είναι η «ροπή της ορμής, ως προς το Ο) .
Δυο παρατηρήσεις:
1) Η στροφορμή ενός υλικού σημείου, που υπολογίζουμε με βάση τα προηγούμενα, αναφέρεται σε μια ορισμένη χρονική στιγμή.
2) Το σημείο αναφοράς Ο, μπορούμε να το πάρουμε σαν την αρχή των αξόνων, σε ένα τρισορθογώνιο σύστημα xyz, χωρίς αυτό να σημαίνει ότι η στροφορμή γενικά, πρέπει να έχει τη διεύθυνση κάποιου από τους τρεις παραπάνω άξονες. Συνεπώς μπορούμε να υποστηρίξουμε ότι η στροφορμή ορίζεται πάντα ως προς την αρχή O ενός συστήματος αναφοράς. Άλλωστε και η ορμή-ταχύτητα ορίζεται ως προς σύστημα αναφοράς και δεν είναι απόλυτα μεγέθη. Έτσι το r του τύπου, δεν είναι τίποτα άλλο, παρά το διάνυσμα θέσης του υλικού σημείου ως προς το σύστημα αναφοράς μας.
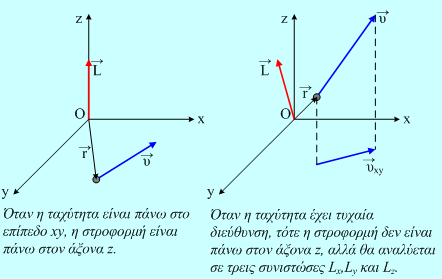
Στον παραπάνω ορισμό δεν αναφερθήκαμε στο είδος της τροχιάς και της κίνησης του υλικού σημείου. Μπορεί να εκτελεί κυκλική, καμπυλόγραμμη, αλλά και να κινείται ακόμη και ευθύγραμμα.
Αν όμως κινείται κυκλικά, τότε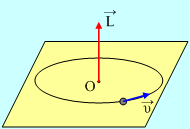 συνήθως η στροφορμή υπολογίζεται ως προς το κέντρο Ο του κύκλου και είναι κάθετη στο επίπεδο της κυκλικής τροχιάς, στο Ο.
συνήθως η στροφορμή υπολογίζεται ως προς το κέντρο Ο του κύκλου και είναι κάθετη στο επίπεδο της κυκλικής τροχιάς, στο Ο.
Έστω τώρα ένα σωματίδιο που στρέφεται ομαλά σε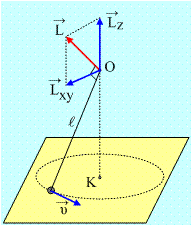 οριζόντιο επίπεδο, δεμένο στο άκρο νήματος μήκους ℓ, διαγράφοντας την παράπλευρη επιφάνεια ενός κώνου, όπως στο σχήμα και θέλουμε την στροφορμή του ως προς το σημείο πρόσδεσης Ο, που βρίσκεται πάνω στην κάθετη στο επίπεδο, στο κέντρο Κ του κύκλου.
οριζόντιο επίπεδο, δεμένο στο άκρο νήματος μήκους ℓ, διαγράφοντας την παράπλευρη επιφάνεια ενός κώνου, όπως στο σχήμα και θέλουμε την στροφορμή του ως προς το σημείο πρόσδεσης Ο, που βρίσκεται πάνω στην κάθετη στο επίπεδο, στο κέντρο Κ του κύκλου.
Με βάση τον προηγούμενο ορισμό έχει σχεδιαστεί το διάνυσμα της στροφορμής στο σχήμα, ενώ το μέτρο της είναι:
«Η συνιστώσα της στροφορμής πάνω στον άξονα z δεν εξαρτάται από τη θέση του σημείου Ο και για όλα τα σημεία του άξονα είναι ΠΑΝΤΑ ίση με Lz=mr2ω, όπου r η απόσταση του σωματιδίου από τον άξονα.»
Συνεπώς μπορούμε να αναφερόμαστε στην στροφορμή του υλικού σημείου κατά τον (και όχι ως προς τον) κάθετο στην τροχιά άξονα z, αλλά δεν πρέπει να ξεχνάμε ότι αυτή είναι μια συνιστώσα της στροφορμής του σωματιδίου και ΟΧΙ η στροφορμή του.
Ας πάρουμε τώρα μια ράβδο μήκους l η οποία στρέφεται με γωνιακή ταχύτητα ω , γύρω από κατακόρυφο άξονα z διαγράφοντας την παράπλευρη επιφάνεια ενός κώνου, όπως στο σχήμα.
Θέλουμε να βρούμε την στροφορμή της ράβδου, ως προς ένα τυχαίο σημείο Ο του άξονα z.
Κάθε υλικό σημείο μάζας mi έχει στροφορμή ως προς το Ο, με κατεύθυνση όπως στο σχήμα (Α) και μέτρο:
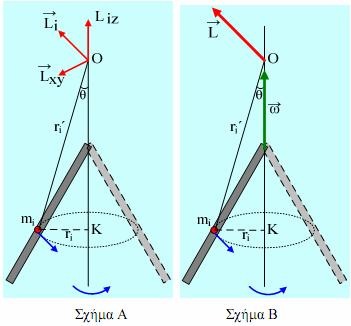
Αν όμως, θέλουμε να βρούμε την συνιστώσα της συνολικής στροφορμής της ράβδουως προς το σημείο Ο, πάνω στον άξονα z, θα έχουμε:
Συμπέρασμα:
Η στροφορμή της ράβδου ως προς το σημείο αναφοράς Ο, δεν έχει την κατεύθυνση του άξονα. Αλλά:
Η προβολή της στροφορμής της ράβδου, πάνω στον άξονα περιστροφής z έχει μέτρο ίσο με:
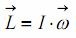
Αφού το διάνυσμα της γωνιακής ταχύτητας είναι πάνω στον άξονα περιστροφής, όχι όμως και το διάνυσμα της στροφορμής, σχήμα (Β).
Και αν είχαμε ένα ομογενές συμμετρικό σώμα το οποίο στρέφεται γύρω από άξονα που περνά από κέντρο μάζας του και είναι άξονας συμμετρίας του;
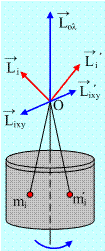 Ας πάρουμε ένα ομογενή κύλινδρο που στρέφεται γύρω από τον άξονα z ο οποίος περνά από τα κέντρα των δύο βάσεών του.
Ας πάρουμε ένα ομογενή κύλινδρο που στρέφεται γύρω από τον άξονα z ο οποίος περνά από τα κέντρα των δύο βάσεών του.
Τότε για κάθε στοιχειώδη μάζα mi υπάρχει και μια ίση συμμετρική της mi΄ που οι στροφορμές τους, ως προς ένα τυχαίο σημείο Ο του άξονα, είναι οι Li και Li΄ όπως φαίνονται στο παρακάτω σχήμα.
Αναλύουμε τις στροφορμές αυτές σε συνιστώσες, οριζόντιες και κατακόρυφες, όπου οι οριζόντιες είναι αντίθετες, δηλαδή:
Για ένα ομογενές συμμετρικό στερεό σώμα που στρέφεται γύρω από έναν άξονα συμμετρίας του, μπορούμε να γράψουμε:
![clip_image014[1] clip_image014[1]](http://lh4.ggpht.com/_BdRE94s86zo/SpJyx5cKG7I/AAAAAAAAHVk/lxK1q7YwDWU/clip_image014%5B1%5D_thumb%5B6%5D.jpg?imgmax=800)
Όπου L η στροφορμή του στερεού ως προς οποιοδήποτε σημείο του άξονα περιστροφής και Ι η ροπή αδράνειας του στερεού ως προς τον άξονα (περιστροφής) συμμετρίας του.
Παράδειγμα:
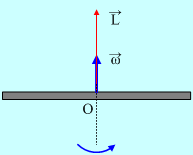
Να υπολογιστεί η (συνολική) στροφορμή μιας ομογενούς ράβδου μάζας Μ και μήκους l η οποία στρέφεται σε οριζόντιο επίπεδο, γύρω από κατακόρυφο άξονα z που περνά από το μέσον της.
Δίνεται η ροπή αδράνειας της ράβδου ως προς τον άξονα Ι=(1/12) Μl2.
Απάντηση:
Με βάση την προηγούμενη ανάλυση, η συνολική στροφορμή της ράβδου, ως προς οποιοδήποτε σημείο του άξονα περιστροφής , έχει την διεύθυνση του άξονα και μέτρο:
L=I·ω= (1/12)Μℓ2·ω.
Αντιπαράδειγμα.
Μια λεπτή ομογενής ράβδος ΑΒ μήκους ℓ και μάζας Μ, στρέφεται σε οριζόντιο επίπεδο, γύρω από κατακόρυφο άξονα z, ο οποίος περνά από το σημείο Μ, όπου (ΑΜ)=0,25ℓ. Να υπολογισθεί η στροφορμή της ράβδου κατά τον άξονα z (δηλαδή η προβολή της στροφορμής πάνω στον z). Δίνεται η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι=(1/12) Μl2.
Απάντηση:
Για κάθε στοιχειώδη μάζα mi μεταξύ του Α και του Μ, υπάρχει η συμμετρική της mi΄μεταξύ του Μ και του Κ (Κ το μέσον της ράβδου). Στο σχήμα έχουν σχεδιαστεί οι στροφορμές για δυο τέτοιες μάζες. Αν r η απόστασή τους από το Ο, αναλύοντας τα διανύσματα των στροφορμών σε οριζόντιες και κατακόρυφες συνιστώσες, παρατηρούμε ότι Lix= - Lix, δηλαδή οι οριζόντιες συνιστώσες αλληλοεξουδετερώνονται.Αλλά κάθε στοιχειώδης μάζα, πέρα του Κ, θα έχει οριζόντια στροφορμή, η οποία θα προστίθεται σε κάθε άλλη παρόμοιας μάζας.
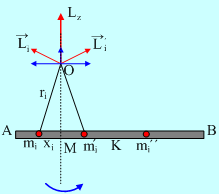
Άρα η στροφορμή της ράβδου ως προς το Ο, θα έχει ΚΑΙ οριζόντια συνιστώσα, δηλαδή συνιστώσα, που δεν θα είναι πάνω στον άξονα περιστροφής z.
Μπορούμε όμως εύκολα να υπολογίσουμε την κατακόρυφη συνιστώσα της στροφορμής, δηλαδή την στροφορμή πάνω στον άξονα περιστροφής z.
1) Η στροφορμή ενός υλικού σημείου, που υπολογίζουμε με βάση τα προηγούμενα, αναφέρεται σε μια ορισμένη χρονική στιγμή.
2) Το σημείο αναφοράς Ο, μπορούμε να το πάρουμε σαν την αρχή των αξόνων, σε ένα τρισορθογώνιο σύστημα xyz, χωρίς αυτό να σημαίνει ότι η στροφορμή γενικά, πρέπει να έχει τη διεύθυνση κάποιου από τους τρεις παραπάνω άξονες. Συνεπώς μπορούμε να υποστηρίξουμε ότι η στροφορμή ορίζεται πάντα ως προς την αρχή O ενός συστήματος αναφοράς. Άλλωστε και η ορμή-ταχύτητα ορίζεται ως προς σύστημα αναφοράς και δεν είναι απόλυτα μεγέθη. Έτσι το r του τύπου, δεν είναι τίποτα άλλο, παρά το διάνυσμα θέσης του υλικού σημείου ως προς το σύστημα αναφοράς μας.

Στον παραπάνω ορισμό δεν αναφερθήκαμε στο είδος της τροχιάς και της κίνησης του υλικού σημείου. Μπορεί να εκτελεί κυκλική, καμπυλόγραμμη, αλλά και να κινείται ακόμη και ευθύγραμμα.
Αν όμως κινείται κυκλικά, τότε
 συνήθως η στροφορμή υπολογίζεται ως προς το κέντρο Ο του κύκλου και είναι κάθετη στο επίπεδο της κυκλικής τροχιάς, στο Ο.
συνήθως η στροφορμή υπολογίζεται ως προς το κέντρο Ο του κύκλου και είναι κάθετη στο επίπεδο της κυκλικής τροχιάς, στο Ο.Έστω τώρα ένα σωματίδιο που στρέφεται ομαλά σε
 οριζόντιο επίπεδο, δεμένο στο άκρο νήματος μήκους ℓ, διαγράφοντας την παράπλευρη επιφάνεια ενός κώνου, όπως στο σχήμα και θέλουμε την στροφορμή του ως προς το σημείο πρόσδεσης Ο, που βρίσκεται πάνω στην κάθετη στο επίπεδο, στο κέντρο Κ του κύκλου.
οριζόντιο επίπεδο, δεμένο στο άκρο νήματος μήκους ℓ, διαγράφοντας την παράπλευρη επιφάνεια ενός κώνου, όπως στο σχήμα και θέλουμε την στροφορμή του ως προς το σημείο πρόσδεσης Ο, που βρίσκεται πάνω στην κάθετη στο επίπεδο, στο κέντρο Κ του κύκλου.Με βάση τον προηγούμενο ορισμό έχει σχεδιαστεί το διάνυσμα της στροφορμής στο σχήμα, ενώ το μέτρο της είναι:
L=mυℓ
Η στροφορμή αυτή αναλύεται σε δύο συνιστώσες, μια οριζόντια Lxyκαι μια κατακόρυφη Lz για την οποία έχουμε:Lz=L∙ημθ=mυℓ∙(r/ℓ) = mυr = mr2ω
Όπου r η ακτίνα της κυκλικής τροχιάς. Παρατηρούμε δηλαδή ότι:«Η συνιστώσα της στροφορμής πάνω στον άξονα z δεν εξαρτάται από τη θέση του σημείου Ο και για όλα τα σημεία του άξονα είναι ΠΑΝΤΑ ίση με Lz=mr2ω, όπου r η απόσταση του σωματιδίου από τον άξονα.»
Συνεπώς μπορούμε να αναφερόμαστε στην στροφορμή του υλικού σημείου κατά τον (και όχι ως προς τον) κάθετο στην τροχιά άξονα z, αλλά δεν πρέπει να ξεχνάμε ότι αυτή είναι μια συνιστώσα της στροφορμής του σωματιδίου και ΟΧΙ η στροφορμή του.
Ας πάρουμε τώρα μια ράβδο μήκους l η οποία στρέφεται με γωνιακή ταχύτητα ω , γύρω από κατακόρυφο άξονα z διαγράφοντας την παράπλευρη επιφάνεια ενός κώνου, όπως στο σχήμα.
Θέλουμε να βρούμε την στροφορμή της ράβδου, ως προς ένα τυχαίο σημείο Ο του άξονα z.
Κάθε υλικό σημείο μάζας mi έχει στροφορμή ως προς το Ο, με κατεύθυνση όπως στο σχήμα (Α) και μέτρο:
Li=miυiri΄.
Συνεπώς η συνολική στροφορμή της ράβδου ως προς το σημείο Ο, θα προκύψει από την σύνθεση όλων των στροφορμών, των στοιχειωδών μαζών από τις οποίες αποτελείται η ράβδος και προφανώς το διάνυσμά της δεν θα έχει την κατεύθυνση του άξονα περιστροφής z σχήμα (Β).
Αν όμως, θέλουμε να βρούμε την συνιστώσα της συνολικής στροφορμής της ράβδουως προς το σημείο Ο, πάνω στον άξονα z, θα έχουμε:
Liz=miυir΄∙ημθ= miυir΄∙(ri/ri΄) = miυiri= miri2∙ω.
Οπότε:
LOz=ΣLiz=Σmiri2∙ω= ω∙Σmiri2= I∙ω
Όπου Ι η ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής z.Συμπέρασμα:
Η στροφορμή της ράβδου ως προς το σημείο αναφοράς Ο, δεν έχει την κατεύθυνση του άξονα. Αλλά:
Η προβολή της στροφορμής της ράβδου, πάνω στον άξονα περιστροφής z έχει μέτρο ίσο με:
Lz= I∙ω (1)
Και αυτό ανεξάρτητα της θέσης του σημείου Ο, ως προς το οποίο την υπολογίσαμε.Βλέπουμε λοιπόν ότι έχει ουσιαστική αξία η στροφορμή ενός στερεού κατά τον άξονα περιστροφής του και η οποία δίνεται από την σχέση (1), αρκεί να θυμόμαστε ότι δεν είναι η στροφορμή ως προς τον άξονα, αλλά η συνιστώσα της στροφορμής πάνω στον άξονα.
Με βάση τα προηγούμενα είναι λάθος να γράψουμε:Αφού το διάνυσμα της γωνιακής ταχύτητας είναι πάνω στον άξονα περιστροφής, όχι όμως και το διάνυσμα της στροφορμής, σχήμα (Β).
Και αν είχαμε ένα ομογενές συμμετρικό σώμα το οποίο στρέφεται γύρω από άξονα που περνά από κέντρο μάζας του και είναι άξονας συμμετρίας του;
 Ας πάρουμε ένα ομογενή κύλινδρο που στρέφεται γύρω από τον άξονα z ο οποίος περνά από τα κέντρα των δύο βάσεών του.
Ας πάρουμε ένα ομογενή κύλινδρο που στρέφεται γύρω από τον άξονα z ο οποίος περνά από τα κέντρα των δύο βάσεών του.Τότε για κάθε στοιχειώδη μάζα mi υπάρχει και μια ίση συμμετρική της mi΄ που οι στροφορμές τους, ως προς ένα τυχαίο σημείο Ο του άξονα, είναι οι Li και Li΄ όπως φαίνονται στο παρακάτω σχήμα.
Αναλύουμε τις στροφορμές αυτές σε συνιστώσες, οριζόντιες και κατακόρυφες, όπου οι οριζόντιες είναι αντίθετες, δηλαδή:
Lixy= - L΄ixy
Συνεπώς η συνολική στροφορμή θα προκύψει από την σύνθεση των συνιστωσών πάνω στον άξονα z για τις οποίες έχουμε:Lολ=ΣLiz=Σmi∙υi∙ri΄∙ημθ= Σ mi∙ω∙xi∙ri΄(xi/ri΄) ή
Lολ=ω∙Σmi∙ri2 = I∙ω.
Συμπέρασμα:Για ένα ομογενές συμμετρικό στερεό σώμα που στρέφεται γύρω από έναν άξονα συμμετρίας του, μπορούμε να γράψουμε:
Όπου L η στροφορμή του στερεού ως προς οποιοδήποτε σημείο του άξονα περιστροφής και Ι η ροπή αδράνειας του στερεού ως προς τον άξονα (περιστροφής) συμμετρίας του.
Παράδειγμα:
Να υπολογιστεί η (συνολική) στροφορμή μιας ομογενούς ράβδου μάζας Μ και μήκους l η οποία στρέφεται σε οριζόντιο επίπεδο, γύρω από κατακόρυφο άξονα z που περνά από το μέσον της.
Δίνεται η ροπή αδράνειας της ράβδου ως προς τον άξονα Ι=(1/12) Μl2.
Απάντηση:
Με βάση την προηγούμενη ανάλυση, η συνολική στροφορμή της ράβδου, ως προς οποιοδήποτε σημείο του άξονα περιστροφής , έχει την διεύθυνση του άξονα και μέτρο:
L=I·ω= (1/12)Μℓ2·ω.

Αντιπαράδειγμα.
Μια λεπτή ομογενής ράβδος ΑΒ μήκους ℓ και μάζας Μ, στρέφεται σε οριζόντιο επίπεδο, γύρω από κατακόρυφο άξονα z, ο οποίος περνά από το σημείο Μ, όπου (ΑΜ)=0,25ℓ. Να υπολογισθεί η στροφορμή της ράβδου κατά τον άξονα z (δηλαδή η προβολή της στροφορμής πάνω στον z). Δίνεται η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι=(1/12) Μl2.
Απάντηση:
Για κάθε στοιχειώδη μάζα mi μεταξύ του Α και του Μ, υπάρχει η συμμετρική της mi΄μεταξύ του Μ και του Κ (Κ το μέσον της ράβδου). Στο σχήμα έχουν σχεδιαστεί οι στροφορμές για δυο τέτοιες μάζες. Αν r η απόστασή τους από το Ο, αναλύοντας τα διανύσματα των στροφορμών σε οριζόντιες και κατακόρυφες συνιστώσες, παρατηρούμε ότι Lix= - Lix, δηλαδή οι οριζόντιες συνιστώσες αλληλοεξουδετερώνονται.Αλλά κάθε στοιχειώδης μάζα, πέρα του Κ, θα έχει οριζόντια στροφορμή, η οποία θα προστίθεται σε κάθε άλλη παρόμοιας μάζας.

Άρα η στροφορμή της ράβδου ως προς το Ο, θα έχει ΚΑΙ οριζόντια συνιστώσα, δηλαδή συνιστώσα, που δεν θα είναι πάνω στον άξονα περιστροφής z.
Μπορούμε όμως εύκολα να υπολογίσουμε την κατακόρυφη συνιστώσα της στροφορμής, δηλαδή την στροφορμή πάνω στον άξονα περιστροφής z.
Lz= ΣLiz= Σ mi∙υi∙ri∙ημθi !
Lz= Σ mi.ω∙xi∙ri∙(xi/ri) = ω∙ Σ mi∙xi2 =Ι∙ω
Συνεπώς η προβολή της στροφορμής πάνω στον άξονα περιστροφής, έχει φορά προς τα πάνω, δεν εξαρτάται από τη θέση του σημείου Ο και έχει μέτρο:Lz= (1/12 Ml2+ 1/16 Ml2) ∙ω = (7/48) Μl2∙ω.
Μπορείτε να το κατεβάσετε σε pdf.

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου